
Morphological filtering is one type of processing in which the spatial form or structure of objects within an image is modified. Dilation, erosion and skeletonization are three fundamental morphological operations.
In this section, we first introduce binary image morphological filtering. Two types of connectivities are defined as following.
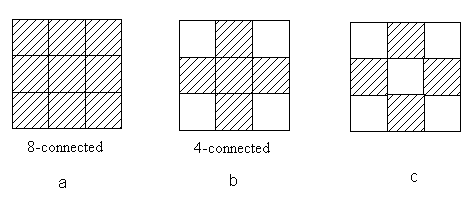
Figure 6.9. Some examples of connectedness
Figure 6.9a illustrates an 8-connectedness while Figure 6.9b shows a 4-connectedness. Under the 8-connected assumption, the structure in Figure 6.9c is a ring while under the 4-connectedness assumption, the structure in Figure 6.9c is not connected.
6.4.1 Binary image hit or miss transformations
Basic morphological operations, dilation, erosion and many variants can be defined and implemented by "hit or miss" transformations. A small odd-sized mask is scanned over a binary image. If the binary-pattern of a mask matches the state of the pixels under the mask, an output pixel in spatial correspondence to the center pixel of the mask is set to some desired binary state. Otherwise, the output is set to the opposite binary state.
For example, to perform simple binary noise cleaning, if the isolated 3 x 3 pixel window
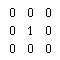
is encountered, the "1" in the center will be replaced by a "0". Otherwise, the center pixel value is not changed.
It is often possible to use simple neighbourhood logical relationships to define the conditions for a hit. For the simple noise removal case,
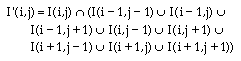
where ![]() denotes the logical and i.e., intersection operation and
denotes the logical and i.e., intersection operation and ![]() denotes the union.
denotes the union.
For simplicity purpose, we use a local coordinates to represent a pixel window:
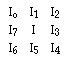
Additive operatorsThe center pixel of a 3 x 3 pixel window are converted by these operators from zero state to one state when a hit is obtained. The basic operators include
Interior Fill - create one if all four-corrected neighbour pixels are one
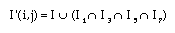
Diagonal Fill - create one if this process will eliminate eight-connecting of the background.
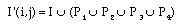
where
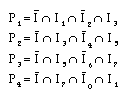
Bridge - Create one if this will result in connectivity of previously unconnected neighbouring ones.
where
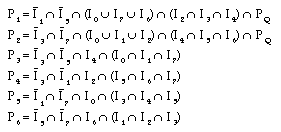
and
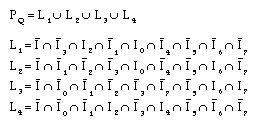
There are 119 patterns which satisfy the above condition. For example,
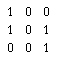
Eight-Neighbour Dilate create one if at least one eight-connected neighbour pixel is one.
Subtractive operators convert center pixel from one to zero.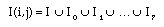
This is a special case of dilation.
Isolated one removalEight-Neighbour Erode - Erase one if at least one eight-connected neighbour pixel is zero.
Spur removal - Erase one with a single eight-connected neighbour
where

H - break - Erase one if it is H-connected

Interior Pixel Removal - Erase one if all 4-connected neighbours are ones
6.4.2 Binary image generalized dilation and erosion
Examples of image set algebraic operations
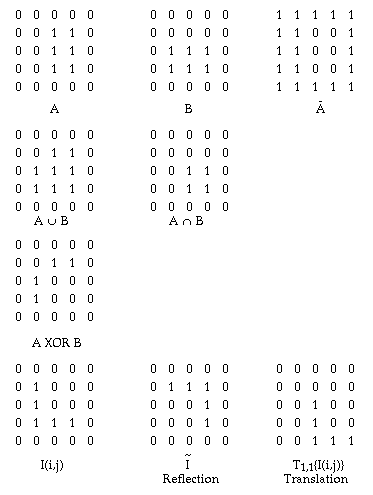
Generalized Dilationwhere I(i,j) for 1 < i, j < N is a binary-valued image and H(m,n) for 1 < m,n < a, a is an odd integer called a structuring element. Minkowski addition is defined asIt is expressed as
In order to compare I(i,j) with I'(i,j). I(i,j) should be translated to
TQ(I(i,j)) where Q = ((L-1)/2, (L-1)/2)Generalized erosion is defined as
where H(m,n) is an odd size LxL structuring element. One formula is
Another formula using the reflection of H as a structuring element:
According to the rules defined above, you can observe what it looks like.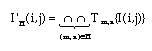
Some properties of Dilation and ErosionDilation is commutativeI(i,j) = I
IBut, in general, erosion is not commutativeJ = J
I
IDilation and erosion are opposite in effect; dilation of a background of an object behaves like erosion of the objectJ
J
I
The following chain rules hold for dilation and erosion
A6.4.3. Binary image close and open operations(B
C) = (A
B)
C
A
(B
C) = (A
B)
C
Dilation and erosion are often applied to an image in concatenation. A dilation followed by an erosion is called a close operation,
I'(i,j) = I(i,j) ï H(m,n) = [I(i,j)The close operation, also called closing, fills gaps and preserves isolated pixels that have a binary value of 1.H(m,n) ]
(m,n)
An erosion followed by a dilation is called an open operation.
I'(i,j) = I(i,j) ï H(m,n) = [I(i,j)The open operation, also called openning, breaks thin connections and clears isolated pixels with binary values of 1.(m,n)]
H(m,n)
6.4.4 Grey scale image morphological filtering
Applying mathematical morphology to grey scale images is equivalent to finding the maximum or the minimum of a neighborhood defined by the structuring element. If a 3X3 neighborhood is taken as a structuring element, then dilation is defined as
I'(i,j) = max (I,I0,I1,I2,I3,I4,I5,I6,I7)
and erosion is defined as
I'(i,j) = min (I,I0,I1,I2,I3,I4,I5,I6,I7).
Similarly, closing refers to a dilation
followed by an erosion while openning means erosion followed by dilation.
The effect of closing on grey scale images is that small objects brighter
than background are preserved and bright objects with small gaps in between
may become connected. Openning, on the other hand, removes bright objects
that are small in size and breaks narrow connections between two bright
objects.
![]()