7.3 Conventional Multispectral Classification Methods
7.3.1 General procedures in image classification
Classification is the most popularly used information extraction techniques in digital remote sensing. In image space I, a classification unit is defined as the image segment on which a classification decision is based. A classification unit could be a pixel, a group of neighbouring pixels or the whole image. Conventional multispectral classification techniques perform class assignments based only on the spectral signatures of a classification unit. Contextual classification refers to the use of spatial, temporal, and other related information, in addition to the spectral information of a classification unit in the classification of an image. Usually, it is the pixel that is used as the classification unit.
General image classification procedures include (Gong and Howarth 1990b):
(1) Design image classification scheme: they are usually information classes such as urban, agriculture, forest areas, etc. Conduct field studies and collect ground infomation and other ancillary data of the study area.
(2) Preprocessing of the image, including radiometric, atmospheric, geometric and topographic corrections, image enhancement, and initial image clustering.
(3) Select representative areas on the image and analyze the initial clustering results or generate training signatures.
(4) Image classification
Supervised mode: using training signature
unsupervised mode: image clustering and cluster grouping
(5) Post-processing: complete geometric correction & filtering and classification decorating.
(6) Accuracy assessment: compare classification results with field studies.
The following diagram shows the major steps in two types of image classification:
Supervised:
Unsupervised
In order to illustrate the differences between the supervised and unsupervised classification, we will introduce two concepts: information class and spectral class:
Information class: a class specified by an image analyst. It refers to the information to be extracted.
Spectral class: a class which includes similar grey-level vectors in the multispectral space.
In an ideal information extraction task, we can directly associate a spectral class in the multispectral space with an information class. For example, we have in a two dimensional space three classes: water, vegetation, and concrete surface.
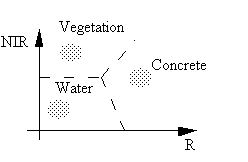
By defining boundaries among the three groups of grey-level vectors in the two-dimensional space, we can separate the three classes.
One of the differences between a supervised classification and an unsupervised one is the ways of associating each spectral class to an information class. For supervised classification, we first start with specifying an information class on the image. An algorithm is then used to summarize multispectral information from the specified areas on the image to form class signatures. This process is called supervised training. For the unsupervised case,however, an algorithm is first applied to the image and some spectral classes (also called clusters) are formed. The image analyst then try to assign a spectral class to the desirable information class.
7.3.2 Supervised classification
Conventional Pixel-Labelling Algorithms in Supervised Classification
A pixel-labelling algorithm is used to assign a pixel to an information class. We can use the previous diagram to discuss ways of doing this.
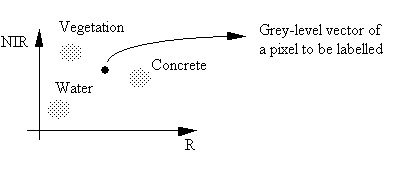
From the above diagram, there are two obvious ways of classifying this pixel.
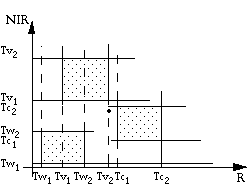
(1) Multidimensional thresholding
As in the above diagram, we define two threshold values along each axis for each class. A grey-level vector is classified into a class only if it falls between the thresholds of that class along each axis.
The advantage of this algorithm is its simplicity. The drawback is the difficulty of including all possible grey-level vectors into the specified class thresholds. It is also difficult to properly adjust the class thresholds.
(2) Minimum-Distance Classification
Fig. 1 shows spectral curves of two types of ground target: vegetation and soil. If we sample the spectral reflectance values for the two types of targets (bold-curves) at three spectral bands: green, red and near-infrared as shown in Fig. 1, we can plot the sampled values in the three dimensional multispectral space (Fig. 2). The sampled spectral values become two points in the multispectral space. Similar curves in Fig. 1 will be represented by closer points in Fig. 2 (two dashed curves in Fig. 1 shown as empty dots in Fig. 2. From Fig. 2, we can easily see that distance can be used as a similarity measure for classification. The closer the two points, the more likely they are in the same class.
We can use various types of distance as similarity measures to develop a classifier, i.e. minimum-distance classifier.
In a minimum-distance classifier,
suppose we have nc known class centers
C = {C1, C2, ..., Cnc}, Ci, i = 1, 2, ..., nc is the
grey-level vector for class i.
As an example, we show a special case in Fig. 3 where we have 3 classes (nc = 3) and two spectral bands (nb = 2)
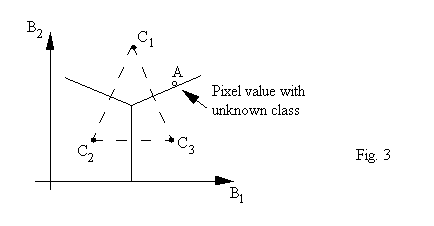
If we have a pixel with a grey-level vector located in the B1-B2 space shown as A (an empty dot), we are asked to determine to which class it should belong. We can calculate the distances between A and each of the centers. A is assigned to the class whose center has the shortest distance to A.
In a general form, an arbitrary pixel with a grey-level vector g = (g1, g2, ..., gnb)T,
is classified as Ci if
d(Ci, g) = min (d(Ci1,g1), d(Ci2,g2), ..., d(Cinb,gnb))
Now, in what form should the distance d take? The most-popularly used form is the Euclidian distance
The second popularly used distance is Mahalanobis distance
where V-1 is the inverse of the covariance matrix of the data.
If the Mahalanobis distance is used, we call the classifier as a Mahalanobis Classifier.
The simplest distance measure is the city-block distance
For dm and de, because taking
their squares will not change the relative magnitude among
distances, in the minimum distance classifiers, we usually use 
as the distance
measures so as to save some computations.
Class centers C and the data covariance matrix V are usually determined from training samples if a supervised classification procedure is used. They can also be obtained from clustering.
For example, there are ns pixels selected as training sample for class Ci.
where j = 1, 2, ..., nb
k = 1, 2, ..., ns
If there are a total of nt pixels selected as training samples for all the classes
The average vector M = (m1, m2, ..., mns) will be obtained.
i = 1, 2, ..., nb.
k = 1, 2, ..., nt.
The covariance matrix is then obtained through the following vector form
(3) Maximum Likelihood Classification (MLC)
MLC is the most common classification method used for remotely sensed data. MLC is based on the Baye's rule.
Let C = (C1, C2, ..., Cnc) denote a set of classes, where nc is the total number of classes. For a given pixel with a grey-level vector x, the probability that x belongs to class ci is P(Ci|x), i = 1, 2, ..., nc. If P(Ci|x) is known for every class, we can determine into which class x should be classified. This can be done by comparing P(Ci|x)'s, i = 1, 2, ..., nc.
x => ci, if P(Ci|x) > P(Cj|x) for all j # i. (1)
However, P(Ci|x) is not known directly. Thus, we use Baye's theorem:
P(Ci|x) = p(x|Ci) ï P(Ci)/P(x)
where
P(Ci) is the probability that Ci occurs in the image. It is called a priori probability.
P(x) is the probability of x occurring in each class ci.
However, P(x) is not needed for the classification purpose because if we compare P(C1|x) with P(C2|x), we can cancel P(x) from each side. Therefore, p(x|Ci) i = 1, 2, ..., nc are the conditional probabilities which have to be determined. One solution is through statistical modelling. This is done by assuming that the conditional probability distribution function (PDF) is normal (also called, Gaussian distribution). If we can find the PDF for each class and the a priori probability, the classification problem will be solved. For p(*x|ci) we use training samples.
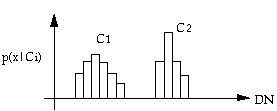
For one-dimensional case, we can see from the above figure that by generating training statistics of two classes, we have their probability distributions. If we use these statistics directly, it will be difficult because it requires a large amount of computer memory. The Gaussian normal distribution model can be used to save the memory. The one-dimensional Gaussian distribution is:
where we only need two parameter
for each class µi and 
, i = 1, 2, ..., nc
µi the mean for Ci
the standard deviation of Ci
µi, can be
easily generated from training sample.
For higher dimensions,
where nb is the dimension (number of bands)
µi is the mean vector of ci
Vi is the covariance matrix of Ci
P(Ci) can also be determined with knowledge about an area. If they are not known, we can assume that each class has an equal chance of occurrence.
i.e. P(C1) = P(C2) = ... = P(Cnc)
With the knowledge of p(x|Ci) and P(Ci), we can conduct maximum likelihood classification. p(x|Ci) ï P(Ci) i = 1, 2, ..., nc can be compared instead of P(Ci|x) in (1).
The interpretation of the maximum likelihood classifier is illustrated in the above figure. An x is classified according to the maximum p(x|Ci) ï P(Ci). x1 is classified into C1, x2 is classified into C2. The class boundary is determined by the point of equal probability.
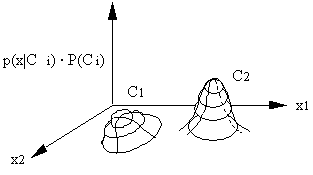
In two-dimensional space, the class boundary cannot be easily determined. Therefore we don't use boundaries in maximum likelihood classification and, instead, we compare probabilities.
Actual implementation of MLC
In order to simplify the computation, we usually take a logarithm of p(x|Ci). P(Ci)
.gif)
Since - nb/2 ï log 2p is a constant, the RHS can be simplified to
(2)
Often, we assume P(Ci) is the same for each class. Therefore (2) can be further simplified to
(3)
g(x) is referred to as the discriminant function.
By comparing g(x)'s, we can assign x to the proper class.
With the maximum likelihood classifier, it is guaranteed that the error of misclassification is minimal if p(x|Ci) is normally distributed.
Unfortunately, the normal distribution cannot always be achieved. In order to make the best use of the MLC method, one has to make sure that his training sample will generate distributions as close to the normal distribution as possible.
How large should one's training sample be? Usually, one needs 10 x nb, preferably 100 x nb, pixels in each class (Swain and Davis, 1978).
MLC is relatively robust but it has the limitation when handling data at nominal or ordinal scales. The computational cost increases considerably as the image dimensionality increases.
For images that the user has little knowledge on the number and the spectral properties of spectral classes, clustering is a useful tool to determine inherent data structures. Clustering in remote sensing is the process of automatic grouping of pixels with similar spectral characteristics.
ï Clustering measures - measures how similar two pixels are. The similarity is based on:
(1) Euclidean distance dE(x1, x2)
(2) City-block distance dc(x1, x2)
ï Clustering criteria - determines how well the clustering results are
ï Sum of Squared Error (SSE)
Clustering algorithm 1: Moving cluster means
K-means clustering (also called c-means clustering)
1. Select K points in the multispectral space as candidate clustering centres
Let these points be
Although m can be arbitrarily selected, it is suggested that they be selected evenly in the multispectral space. For example, they can be selected along the diagonal axis going through the origin of the multispectral space.
2. Assign each pixel x in the image to the closest cluster centre m
3. Generate a new set of cluster centers based on the processed result in 2.
n is the number of iterations of step 2.
4. If
,(a small tolerance), the procedure is terminated. Otherwise let
=
and return to step 2 to continue.
Clustering Algorithm 2
ISODATA - Iterative Self Organizing Data Analysis Technique A
Based on the K-means algorithm, ISODATA adds two additional steps to optimize the clustering process.
1. Merging and deletion of clusters
At a suitable stage, e.g. after a number of iterations of steps 2 - 4 in the K-means algorithm, all the clusters
i = 1, 2, ..., nc are examined.
If the number of pixels in a particular cluster is too small, then that particular cluster is deleted.
If two clusters are too close, then they are merged into one cluster.
2. Splitting a cluster
If the variance of a cluster is too large, that cluster can be divided into two clusters.
These two steps increase the adaptivity of the algorithm but also increase the complexity of computation. Compared to K-means, ISODATA requires more specification of parameters for deletion and merging and a variance limit for splitting. Variance has to be calculated for each cluster.
In the K-means algorithm, clustering may not be realized, i.e., the clustering is not converging. Therefore, we might have to specify the number of iterations to terminate a clustering process.
Clustering Algorithm 3: Hyrarchical clustering.
This algorithm does not require an image analyst to specify the number of classes beforehand. It assumes that all pixels are individual clusters and systematically merges clusters by checking distances between means. This process is continued until all pixels are in one cluster. The history of merging (fusion) is recorded and they are displayed on a dendrogram, which is a diagram that shows at what distances the centers of particular clusters are merged. The following figure shows an example of this algorithm.
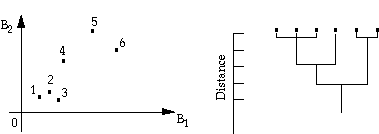
This procedure is rarely used in remote sensing because a relatively large number of pixels in the initial cluster centers requires a huge amount of disk storage in order to keep track of cluster distances at various levels. However, this algorithm can be used when a smaller number of clusters is obtained previously from some other methods.
Clustering Algorithm 4: Histogram-based clustering.
Histogram in high dimensional
space 
H(V) is the occurrence frequency of
grey-level vector V. The algorithm is to find peaks in the multi-
dimensional histogram: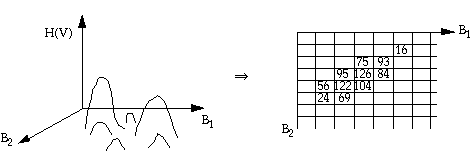
(1) Construct a multi-dimensional histogram
(2) Search for peaks in the multispectral space using an eight-neighbour comparison strategy to see if the center frequency is the highest in a 3 x 3 grey-level vector neighbourhood. For three dimensional space, search the peak in a
neighbourhood.
(3) If a local highest frequency grey-level vector is found, it is recorded as a cluster center.
(4) After all centers are found, they are examined according to the distance between each pair of clusters. Certain clusters can be merged if they are close together. If a cluster center has a low frequency it can be deleted.
The disadvantage of this algorithm is that it requires a large amount of memory space (RAM). For an 8-bit image, we require 256 x 4 bytes to store frequencies (each frequency is a 40 byte integer) if the image has only one band. As the dimensionality becomes higher, we need x 4 bytes of memory. When NB = 3, it requires 64 MB (256nb). Nevertheless, this limit could partly be overcome by a grey-level vector reduction algorithm (Gong and Howarth, 1992a).
Accuracy assessment of remote sensing product
The process from remote sensing data to cartographic product can be summarized as following:
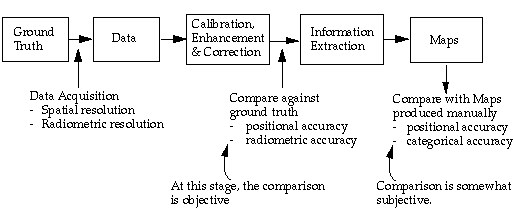
The reference that the remote sensing products are to be compared with is created based on human generalization. Depending on the scale of the reference map product, linear features and object boundaries are allowed to have a buffer zone. As long as the boundaries fall in their respective buffer zones, they are considered correct.
However, this has not been the case in assessing remote sensing products. In the evaluation of remote sensing products, we have traditionally adopted a hit-or-miss approach, i.e., by overlaying the reference map on top of the map product obtained from remote sensing, instead of giving the RS products tolerant buffers.
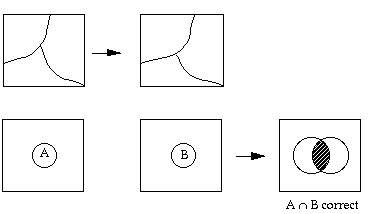
Some of the classification accuracy assessment algorithms can be found in Rosenfield and Fitz patrick-lins (1986) and Story and Congalton (1986)
In the evaluation of classification errors, a classification error matrix is typically formed. This matrix is sometimes called confusion matrix or contingency table. In this table, classification is given as rows and verification (ground truth) is given as columns for each sample point.
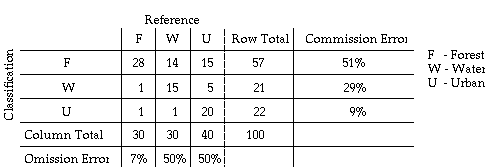
The above table is an example confusion matrix. The diagonal elements in this matrix indicate numbers of sample for which the classification results agree with the reference data.
The matrix contain the complete information on the categorical accuracy. Off diagonal elements in each row present the numbers of sample that has been misclassified by the classifier, i.e., the classifier is committing a label to those samples which actually belong to other labels. The misclassification error is called commission error.
The off-diagonal elements in each column are those samples being omitted by the classifier. Therefore, the misclassification error is also called omission error.
In order to summarize the classification results, the most commonly used accuracy measure is the overall accuracy:
From the example of confusion
matrix, we can obtain 
= (28 + 15 + 20)/100 = 63%.
More specific measures are needed because the overall accuracy does not indicate how the accuracy is distributed across the individual categories. The categories could, and frequently do, exhibit drastically differing accuracies but overall accuracy method considers these categories as having equivalent or similar accuracies.
By examining the confusion matrix, it can be seen that at least two methods can be used to determine individual category accuracies.
(1) The ratio between the number of correctly classified and the row total
(2) The ratio between the number of correctly classified and the column total
(1) is called the user's accuracy because users are concerned about what percentage of the classes has been correctly classified.
(2) is called the producer's accuracy.
The producer is more interested in (2) because it tells how correctly the reference samples are classified.
However, there is a more appropriate way of presenting the individual classification accuracies. This is through the use of commission error and omission error.
Commission error = 1 - user's accuracy
Omission error = 1 - producer's accuracy
Kappa coefficient
The Kappa coefficient (K) measures the relationship between beyond chance agreement and expected disagreement. This measure uses all elements in the matrix and not just the diagonal ones. The estimate of Kappa is the proportion of agreement after chance agreement is removed from consideration:
= (po - pc)/(1 - pc)
po = proportion of units which agree, =Spii = overall accuracy
pc = proportion of units for expected chance agreement =Spi+ p+i
pij = eij/NT
pi+ = row subtotal of pij for row i
p+i = column subtotal of pij for column i
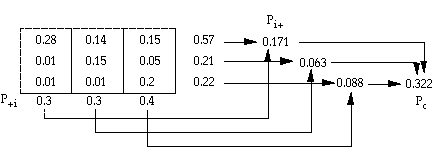
po = 0.63
One of the advantages of using
this method is that we can statistically compare two
classification products. For example, two classification maps can
be made using different algorithms and we can use the same
reference data to verify them. Twos can be derived, 1,
2. For
each, the
variance 
can
also be calculated.
It has been suggested that a z-score be calculated by
A normal distribution table can be
used to determine where the two s are significantly different from Z.
e.g. if Z> 1.96, then the difference is said to be significant at the 0.95 probability level.
can be
estimated by using the following equation:
Given the above procedures, we need to know how many samples are need to be collected and where they should be placed.
Sample size
(1) The larger the sample size, more representative an estimate can be obtained, therefore, more confidence can be achieved.
(2) In order to give each class a proper evaluation, a minimum sample size should be applied to every class.
(3) Researchers have proposed a number of pixel sampling schemes (e.g., Jensen, 1983). These are:
ï Random
ï Stratified Random
ï Systematic
ï Stratified Systematic Unaligned Sampling
